首先明确一个概念,电磁波具有波粒二象性,因而电磁波在空间中是以波的形式传播的。
电磁波在真空中速度根据麦克斯韦方程组可以得到等于光速:3.0*10^8m/s,但一定记住这是在真空中的速度
由于波的性质,电磁波在各种介质中的传播速度是不一样的,传播速度公式:
V=C/n=λ*f
C-真空中的光速3.0*10^8m/s
n-介质的介电常数
回顾前面章节的学习我们可以知道,MR发射的RF射频信号是有固定频率的,而这个频率与MR系统的磁场强度直接相关。我们可以把人体看成是水组成的,那么有了频率,有了速度很简单我们就能够计算出来MR发射的射频信号进入人体后电磁波的波长。不同磁场强度的系统电磁波在人体中的波长如下:

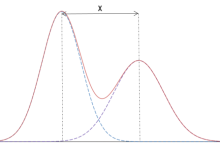
驻波 (standing wave) 频率相同、传输方向相反的两种波(不一定是电磁波),沿传输线形成的一种分布状态。其中的一个波一般是另一个波的反射波。
在两者电压(或电流)相加的点出现波腹,在两者电压(或电流)相减的点形成波节。
在波形上,波节和波腹的位置始终是不变的,给人驻立不动的印象,所以称作驻波。
当驻波形成时,无论怎么看叠加波形的波腹和波节始终都在同一个位置,好像矗立不动了,说起来比较抽象,大家参考下面的动态图自行理解。
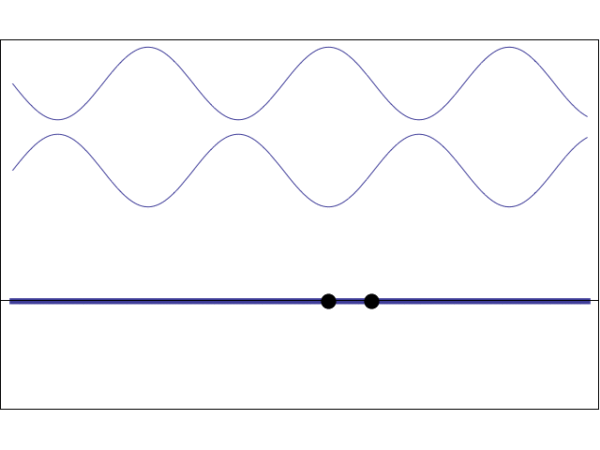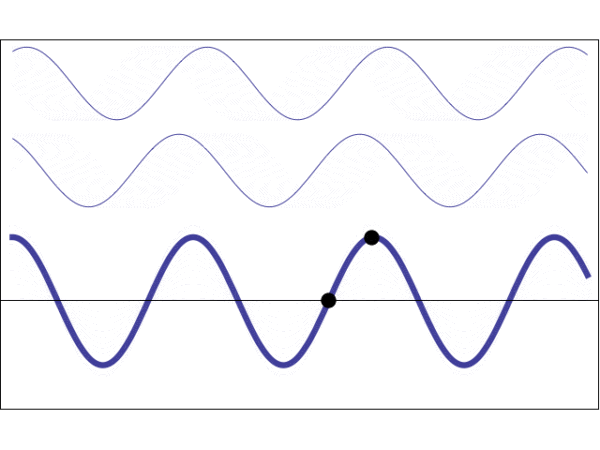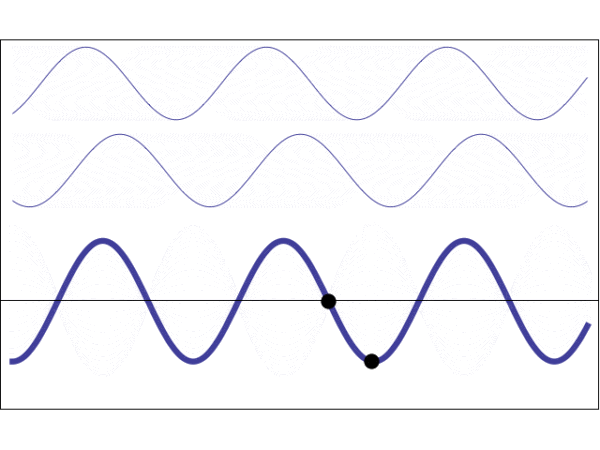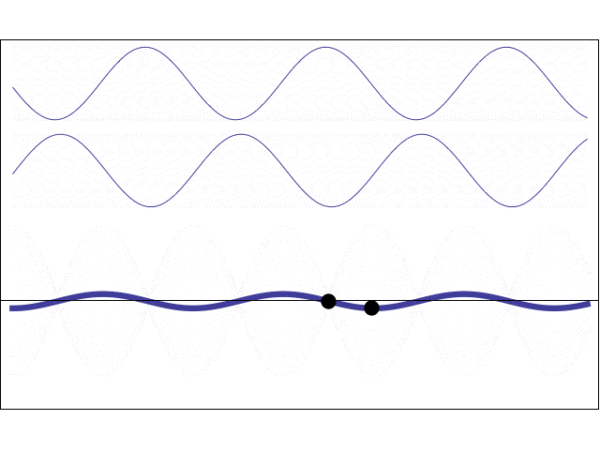
而对于一般低频信号来说,由于波长很长,人体的截面与它相比所占比例很小,所以在人体范围内波动的起伏并不大。
但是当频率提高,波长减小,波长正好与人体宽度接近时,人体宽度范围内波形呈现波节与波腹的巨大差距。而且由于驻波,波腹与波节始终在同一位置。
参考各种磁场强度下射频传播波长,可以发现3.0T的系统波长是26cm,基本等于人体横截面的宽度,因此在这种条件下,RF射频信号很容易在人体中产生驻波。
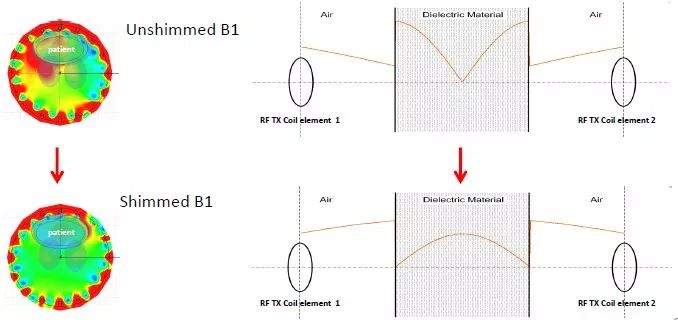
而驻波导致的结果就是射频在人体内发生了不均匀,这种不均匀反映到最终的图像上就会出现黑影区域,也就是介电伪影。
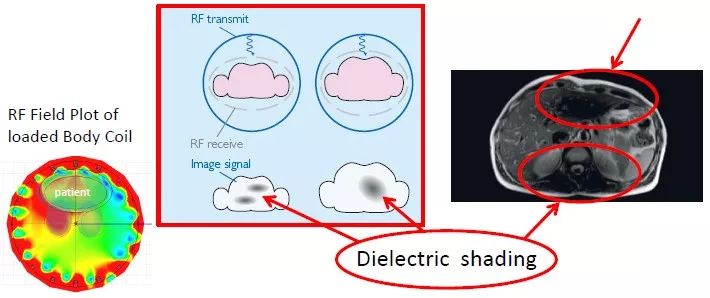
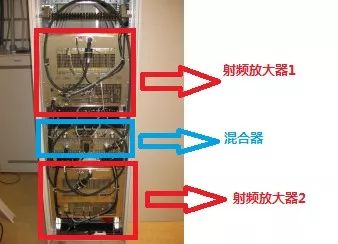
由于人体的截面肯定无法改变,射频的波长也无法改变,射频的速度也无法改变,所以单一射频场无法解决介电伪影问题。那么用两路射频呢?因此双射频发射技术(MultiTransmit)应运而生。
假设一路射频1入射到人体中会产生相应的驻波,既然驻波1的波节位置是固定的,那么我们使用另一路射频2入射到人体,通过控制正好让驻波2的波节位置发生在驻波1的波腹处,这样射频能量就会重新均匀。
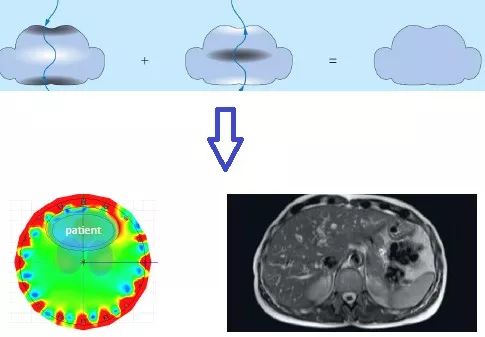
B1 shimming或者RF shimming。